Booleovská algebra. Časť 2. Základné zákony a funkcie

Pokračovanie príbehu o booleovskej algebre, konvenciách, pravidlách, operáciách. Prechod na základy kontaktných obvodov.

prvý článok George Bull bol opísaný ako tvorca algebry logiky. V druhom článku sa opíšu základné operácie booleovskej algebry a metódy na zjednodušenie booleovských výrazov. Boolovská algebra teda používa výroky ako argumenty a nie ich význam, ale pravdivosť alebo nepravdivosť výroku.

Formulár na písanie výrazov v booleovskej algebre.

Ak je tvrdenie pravdivé, píše sa takto: A = 1, ak je nepravdivé, potom A = 0 (napokon nie je pravda, že zemiaky sú ovocie). Pre každé tvrdenie je A buď true (A = 1) alebo false (A = 0). Stred tu nemôže byť. O tom sme už hovorili.

Ak spojíte dva jednoduché príkazy s jednotkou A, získate komplexné vyhlásenie, ktoré sa nazýva logický produkt. Urobme dva jednoduché výroky: „Tri sú viac ako dva“ označíme písmenom A, „Tri menej ako päť“ - písmenom B.

Preto je komplexné tvrdenie „tri je viac ako dva a menej ako päť“ logické (v tomto prípade veľké písmeno A hovorí, že ide o logickú operáciu „AND“, ako aj neskôr v texte „ALEBO“ a „NIE“). a B. Označuje sa takto: A ^ B alebo A * B.

Logické násobenie (operácia „AND“).

V elementárnej algebre A * A = A2. Ale v Buhlovej algebre A * A = A2 = A, A * A = A, pretože znamienko násobenia (*) teraz znamená ... A ... v zmysle And ... A. Všetky naše skúsenosti potvrdzujú, že A&A sú rovnaké ako v prípade samotného A. S tým nemôžeme nesúhlasiť. Pravda výroku sa nemení, ak sa niekoľkokrát opakuje.

Produkt dvoch výrokov sa potom považuje za pravdivý (rovný 1) a iba vtedy, ak sú oba faktory pravdivé, a nepravdivý (rovný 0), ak je aspoň jeden z týchto faktorov nepravdivý. Súhlasí s tým, že tieto pravidlá nie sú v rozpore so zdravým rozumom a okrem toho sú v úplnom súlade s pravidlami základnej algebry:

1*1 = 1, 1*0 = 0 = 0*1 = 0, 0*0 = 0.

Prvá rovnosť znie takto: ak sú A aj B pravdivé, potom platí produkt A * B. V Buhlovej algebre znak násobenia (*) nahrádza spojenie I.

Logické produkty môžu obsahovať nie dva, ale väčší počet tvrdení - faktorov. A v tomto prípade je produkt pravdivý iba vtedy, keď sú pravdivé všetky tvrdenia a faktory.

Logické sčítanie (ALEBO operácia)

Ak sú dve vyhlásenia spojené zväzom ALEBO. táto vytvorená zložená veta sa nazýva logická suma.

Zoberme si príklad logického súčtu. Hovorí: „Dnes pôjdem do kina.“

Vyhlásenie B: „Dnes pôjdem na diskotéku.“ Pridáme obe vyhlásenia a dostaneme: „Dnes pôjdem k filmom ALEBO na diskotéku.“

Toto komplexné tvrdenie sa označuje takto: A + B = C alebo (A V B) = C.

C označili komplexné vyjadrenie logickej sumy.

V uvažovanom príklade nie je možné zväzok ALEBO použiť v exkluzívnom zmysle. V ten istý deň sa naozaj dostanete do kina a na diskotéku. A tu je príslovie:

„Predsedom záhradníckeho partnerstva bude Petrov alebo Ivanov,“ nie je logická suma, pretože predsedom bude iba jedna osoba a druhá amatérsky bežný záhradník.

Znamienko V pre logický súčet sa zvolí preto, že je na rozdiel od latinského slova „aut>, čo znamená„ a “, počiatočným písmenom latinského slova„ vel “, čo znamená„ alebo “. Teraz by malo byť každému jasné, prečo je logický produkt označený znakom ^.

V elementárnej algebre existuje pravidlo A + A = 2A. Toto pravidlo je pravdivé, bez ohľadu na to, aké číslo predstavuje písmeno A. V booleovskej algebre tomu zodpovedá pravidlo A + A = A. Celá naša životná skúsenosť hovorí, že povedať A ALEBO alebo obidve A je len ďalší a dlhší spôsob, ako povedať len A.

Rovnako ako každé zložené vyhlásenie, súčet oboch vyhlásení A a B môže byť pravdivý alebo nepravdivý. Suma sa považuje za pravdivú, tj rovná sa jednote, ak je pravdivá aspoň jedna z týchto podmienok:

A + B = 1, ak OR A = 1 alebo B = 1, čo je v súlade s konvenčnou aritmetikou:

1+0 = 0+1 = 1.

Ak sú obidva sčítané príkazy pravdivé, potom sa suma považuje za pravdivú, preto v booleovskej algebre máme: (1) + (1) = 1.

Zátvorky sú tu uvedené, aby zdôraznili podmienenosť, význam tohto doplnku, a nie aritmetické.

Súčet dvoch výrokov sa považuje za nepravdivý a rovný nule, ak, ale iba ak sú oba výrazy nepravdivé. Odtiaľto:

0 + 0=0.

Súčet týchto dvoch výrokov A + B sa teda považuje za pravdivý, ak je pravdivý, OR A, OR B alebo OR spolu. Slovo OR je teda označené +.

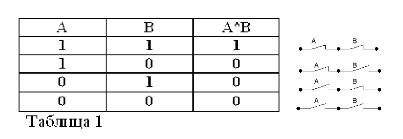
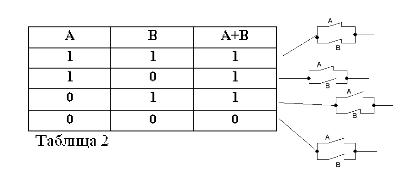
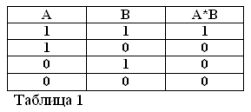
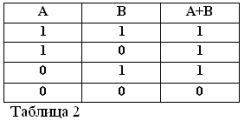
Pamätajúc na to, že výroky A a B môžu byť iba pravdivé alebo nepravdivé, a preto majú mieru pravdy 1 alebo 0, výsledky zvažovaných operácií AND a OR možno zhrnúť v tabuľkách 1 a 2.

Treťou operáciou, ktorú Buhlova algebra často používa, je negačná operácia - NIE. Pripomíname vám, že elementárna algebra používa operácie ADD, D Subtract, Multiply by, Delte by a niektoré ďalšie.

Pre každé vyhlásenie A existuje jeho negácia NOT A, ktorú označíme symbolom / A. To by nemalo byť pochýb.

Uvádzame príklady: „Pôjdeme do lesa“ A, „Nepôjdeme do lesa“ / A.

Ak je tvrdenie A pravdivé, tj A = 1, potom jeho negácia / A musí byť nepravdivá / A = 0. A naopak, ak je akékoľvek tvrdenie nepravdivé, potom je jeho negácia pravdivá. Napríklad: „Kôň neje seno“ / A = 0, „Kôň neje seno“ (A = 1). Toto možno vyjadriť v tabuľke 3.

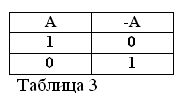
Stanovenie významu akcie negácie a za predpokladu, že z oboch výrokov A a / A je vždy jedno pravdivé, nasledujú dve nové vzorce booleovskej algebry:

A + (/ A) = 1 a A * (/ A) = 0.

Existujú aj iné vzorce, ktoré zjednodušujú logické spracovanie príkazov. Napríklad 1 + A = 1, pretože podľa definície sčítania v prípade, keď sa jeden člen rovná jednote, suma sa vždy rovná jednote. Získaný výsledok nezávisí od toho, či A = 0 alebo A = 1.

Každá z troch logických operácií, ktoré sme skúmali (A, ALEBO, NIE) má určité vlastnosti, ktoré sú blízke pravidlám elementárnej algebry. Ak sú všetky formulované, dostaneme 25 pravidiel booleovskej algebry. Sú dosť na to, aby vyriešili takmer akýkoľvek logický problém. Bez týchto pravidiel je dosť zložité riešiť logické problémy z dôvodu ich zjavnej zložitosti. Pokúsiť sa nájsť správnu odpoveď bez použitia pravidiel znamená nahradiť ich vynaliezavosťou a všeobecným odôvodnením. Pravidlá veľmi uľahčujú túto prácu a šetria čas.

V rámci tohto článku nie je možné vziať do úvahy všetkých týchto 25 pravidiel, ale tí, ktorí si to želajú, ich vždy nájdu v príslušnej literatúre.

Ako už bolo spomenuté v prvom článku v roku 1938, mladý americký vedec Claude Shannon vo svojom článku „Symbolická analýza reléových a spínacích obvodov“ prvýkrát používa booleovskú algebru na problémy s technológiou prenosu. Shannon objav bol, že si uvedomil, že metóda navrhovania reléových strojov a elektronických počítačov je v skutočnosti odvetvím matematickej logiky.

Často sa to stáva. Vedec už mnoho rokov pracuje na probléme, ktorý sa zdá, že jeho krajanom je úplne zbytočný - len zábava. Prejdú však desaťročia a niekedy aj storočia a teória, ktorú nikto nepotrebuje, nezískava len právo na existenciu, ale bez neho sa ďalší pokrok stane nemysliteľným.

Čo pomohlo Shannonovi druhýkrát „objaviť“ booleovskú algebru? Prípad? Nič také.

Láska k reléovým strojom postaveným na konvenčných spínačoch a relé pomohla mladému vedcovi spojiť zabudnutú teóriu s úlohami automatických telefónnych ústrední, na ktorých v tom čase pracoval. Následne Shannon predstavil tú istú myšlienku „áno alebo nie“ v diskrétnych správach a položil základy celej časti kybernetiky - informačnej teórie.

Buhlova algebra bola veľmi vhodná na analýzu a syntézu reléových obvodov. Stačilo akceptovať ako pravdivé vyhlásenie: „V obvode je signál“ a ako falošný - „V obvode nie je žiadny signál“, ako sa objavila nová algebra - signálna algebra, algebra reléového obvodu.

Nová algebra je platná iba pre posúdenie relé a spínacích obvodov. Koniec koncov, iba v takýchto schémach je splnená podmienka „existuje signál“ a „žiadny signál“. Ak sa signál mení nepretržite a získava ľubovoľne veľký počet stredných podmienok (taký signál sa nazýva analógový), reléová algebra sa neuplatňuje. Toto sa musí vždy pamätať. Ale iba väčšina elektronických počítačov a kybernetických strojov používa diskrétny princíp spracovania signálu, ktorý je založený na prvkoch „áno - nie“.

Shannon akceptoval výraz „kontakt uzavretý“ ako pravdivý (1) a „kontakt otvorený“ ako nepravdivý (0). Zvyšok „algebry“ vrátane operácií AND, OR, NOT a 25 pravidiel si Shannon požičal od Boole.

Algebra reléového obvodu sa ukázala byť jednoduchšia ako booleovská algebra, pretože sa zaoberá iba prvkami typu „áno - nie“. Nová algebra je navyše vizuálnejšia.

Prvkami v tejto algebre sú kontakty, ktoré označíme písmenami A, B, C ... Kontakt je uzavretý - A, kontakt je otvorený - / A (písmeno s pomlčkou).

Ako vidíte, zápis je úplne prevzatý z booleovskej algebry. Otvorený kontakt je negácia uzavretého kontaktu. Ten istý kontakt nemôže byť uzavretý aj otvorený.

Súhlasíme, že ak sú v ktoromkoľvek obvode dva kontakty označené rovnakým písmenom, znamená to, že vždy berú rovnaké hodnoty.

V ktoromkoľvek danom okamihu sú obidve otvorené súčasne alebo obidve sú zatvorené. Najjednoduchší spôsob, ako si ich predstaviť, sú navzájom mechanicky spojené tak, aby sa obidva súčasne otvorili alebo zatvorili.

Ak je kontakt v niektorom reťazci negáciou iného kontaktu, ich význam je vždy opačný. Napríklad kontakty C a / C nemôžu byť nikdy otvorené súčasne alebo súčasne zatvorené. A v diagrame môžu byť znázornené mechanicky spojené: ak sa jeden z nich otvorí, druhý sa zatvorí.

Naše zoznámenie sa s reléovou algebrou začneme analýzou najjednoduchších obvodov zodpovedajúcich operáciám AND, OR a NOT.

Produkt dvoch kontaktov (operácia AND) je obvod získaný ako výsledok ich sériového zapojenia: je uzavretý (rovná 1) iba vtedy, keď sú oba kontakty zatvorené (rovné 1).

Súčet dvoch kontaktov (operácia OR) bude obvodom vytvoreným, keď sú zapojené paralelne: je uzavretý (rovná 1), keď je uzavretý aspoň jeden z kontaktov tvoriacich obvod (rovný 1).

Opak tohto kontaktu (operácia NIE) je kontakt rovný 0 (otvorený), ak je tento kontakt 1 (zatvorený), a naopak.

Rovnako ako v booleovskej algebre, ak sú kontakty označené písmenami A a B, označíme súčin dvoch kontaktov A * B, súčet A + B a kontakt opačný A, podľa / A. Vyššie uvedené je vysvetlené na obrázkoch 1, 2 a 3.

Platnosť tabuliek zodpovedajúcich operáciám AND, OR a NOT. teraz by nikto nemal mať pochybnosti.

Budeme sa zaoberať dvoma príkladmi: 1 * 0 = 0 a 1 + 0 = 1.

Z obrázku je zrejmé, že trvalo uzavretý kontakt zapojený do série s trvalo otvoreným kontaktom je ekvivalentom trvalo otvoreného kontaktu (1 * 0 = 0). Trvale zatvorený kontakt spojený paralelne s trvalo otvoreným kontaktom je ekvivalentom trvalo uzavretého kontaktu.

Po zoznámení sa s aritmetikou kontaktných obvodov môžete opísať akýkoľvek reléový obvod pomocou vzorca pomocou akceptovaných konvencií. V kybernetike sa takéto vzorce nazývajú štrukturálne.

Ak štruktúrny vzorec ktoréhokoľvek reléového obvodu je 1, potom ním môže prechádzať signál - obvod je uzavretý. A naopak, ak je štruktúrny vzorec obvodu 0, signál ním neprechádza - obvod je prerušený.Záver: dva reléové obvody sú si navzájom rovnocenné, ak sú ich štruktúrne vzorce rovnaké.

V ďalšej časti článku sa budeme zaoberať príkladmi kontaktných obvodov, typických kontaktných obvodov a ich ekvivalentov, ako aj vypracovaním schém podľa štruktúrnych vzorcov. Zohľadňujeme tiež hlavné logické obvody, ktoré vykonávajú funkcie booleovskej algebry.

Pokračovanie článku: Booleovská algebra. Časť 3. Kontaktné schémy

Boris Aladyshkin

Comments

[#1 alex]

Ďakujem

Iba jeden bod, odsek:

"Rovnako ako v booleovskej algebre, ak sú kontakty označené písmenami A a B, označíme súčin dvoch kontaktov A * B, súčet A + B a kontakt opačný A, podľa / A. To je vysvetlené na obrázkoch 1, 2 a 3 ..."

Kde je obrázok 3?