Booleovská algebra. Časť 1. Trocha histórie

V škole sme všetci študovali algebru, ale nehovorili o booleovskej algebre. V tomto článku je opísaný rozdiel medzi booleovskou algebrou a školskou algebrou, históriou jej vzhľadu, problémami a aplikáciami.

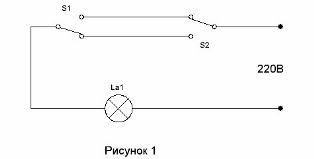
Okruh, ktorý umožňuje dvom spínačom zapnúť svetlo v chodbe pri vstupe do chodby a vypnúť ho pri vstupe do miestnosti, je známy už veľmi dlho (pozri. Obvod riadenia obvodu koridoru). Je to znázornené na obrázku 1.

Úloha číslo 1, Zložitejšie. Vytvorte schému, ktorá vám umožní zapnúť a vypnúť svetlo vo vašej miestnosti pomocou 3 rôznych prepínačov. Spínače sú umiestnené pri vchode do miestnosti, nad posteľou a pri stole.

Úloha číslo 2.

V športovom výbore, napríklad vo výrobnom výbore, sa zišlo 5 sudcov.

Každý z nich musí hlasovať za iné rozhodnutia. Rozhodnutie sa prijíma väčšinou hlasov, ale iba za podmienky, že za to hlasuje predseda výboru.

Sudcovia hlasujú stlačením tlačidla, ktoré uzatvára spínač umiestnený pod stolom, na ktorom sedí. Uzatvorením prepínača hlasovali za, pričom sa záporné hodnoty odpojili. Nakreslite jednoduchý diagram, ktorý vám umožní automaticky zobraziť výsledky hlasovania. V najjednoduchšom prípade jednoducho pomocou žiarovky - svieti - bolo prijaté rozhodnutie, nesvietilo - nie.

Úloha číslo 3, V praxi je to nepravdepodobné, ale ako zložitá vzdelávacia úloha je celkom vhodná.

Vo veľkej šesťuholníkovej miestnosti je na každej stene nainštalovaný jeden spínač. Zostavte obvod tak, že kedykoľvek môžete zapnúť alebo vypnúť svetlo v miestnosti otočením jedného (ľubovoľného) spínača.

Keď neúspešne sedíte nad úlohami tri až štyri dni, dočasne ich odložte. A zaneprázdnený Booleovská algebra, Je to booleovská algebra alebo, ako sa tiež nazýva, Booleovská algebra, algebra reléového obvodu, pomôžu vám vyriešiť vaše problémy.

Čo je booleovská algebra?

Je zvláštne, že napriek tomu, že už päť rokov študujú algebru v škole, veľa študentov a neskôr dospelí nebudú schopní odpovedať na otázku, čo je algebra? Algebra je veda, ktorá študuje súbory niektorých prvkov a akcie s nimi.

V školskom kurze algebry sú také prvky čísla. Čísla nie je možné označovať číslami, ale písmenami, každý to pozná. V prvých hodinách algebry to pre mnohých študentov vždy sťažuje. Pamätajte, aké ťažké bolo spočiatku zvyknúť si na pridávanie písmen namiesto čísel, riešenie rovníc, ktoré nehovoria nič.

Pravdepodobne si každý z nás položil otázku: „Prečo musíme namiesto čísel zadávať písmená a je to vôbec potrebné?“ Až neskôr ste videli, aké výhody algebra prináša pri riešení problémov v porovnaní s aritmetikou.

Algebra sa používa v mnohých presných vedách. Toto je fyzika, mechanika, sopromat, elektrina. Ohmov zákon neexistuje nič viac ako algebraická rovnica: stačí nahradiť ich numerické hodnoty namiesto písmen, aby sme zistili, aký prúd bude prúdiť v záťaži alebo aký odpor má časť obvodu.

Takže ste sa zoznámili s algebrou čísel alebo s elementárnou algebrou. Hlavnou a takmer jedinečnou úlohou je získať odpoveď na otázku: „Čo sa rovná X? Koľko? “

Na strednej škole študujú začiatky vektorovej algebry. Táto algebra sa zásadne líši od základnej algebry. Má odlišný charakter skúmaného súboru a iných pravidiel činnosti. Pri riešení vektorovej rovnice dostaneme v odpovedi vektor, ktorý nie je bežné číslo, ktoré odpovedá na otázku „Koľko?“

Vzorce vektorovej algebry sa v mnohých ohľadoch líšia od vzorcov elementárnej algebry. Napríklad v elementárnej algebre a vo vektorovej algebre existuje operácia sčítania. Vykonáva sa však úplne iným spôsobom.Sčítanie čísel nie je vôbec rovnaké ako sčítanie vektorov.

Existujú aj ďalšie algebry: lineárna algebra, algebra štruktúr, algebra prsteňov, algebra logiky alebo, čo je to isté, logická algebra. Pravdepodobne ste nepočuli meno v školských hodinách. George Boole - ale každý pozná meno jednej zo svojich talentovaných dcér Ethel Voinich (1864 - 1960). Napísala román Gadfly, ktorý hovorí o boji za práva talianskych karbonárov.

George Bull sa narodil v Anglicku 2. novembra 1815. Celý život pôsobil ako učiteľ matematiky a fyziky v škole. Z spomienok jeho študentov je známe, aký veľký význam prikladal Bul rozvoju tvorivých schopností študentov. Pri prezentácii nového materiálu sa snažil zabezpečiť, aby jeho študenti sami „znovuobjavili“ určité vzorce a zákony.

Učiteľ rozprával študentom o ťažkostiach, ktorým vedci nevyhnutne čelili pri hľadaní pravdy. Učiteľ rád opakoval jednu východnú múdrosť: ani perzský trón nemôže človeku priniesť toľko potešenia ako najmenší vedecký objav. Buhl nikdy nestratil nádej, že jedného dňa jeho študenti urobia skutočný objav.

Rozsah vedeckých záujmov Buhl bol veľmi široký: rovnako sa zaujímal o matematiku a logiku - veda o zákonoch a formách myslenia. V tých časoch sa logika považovala za humanitárnu vedu a mnohí, ktorí vedeli, že George Boole bol ohromený tým, ako presné metódy poznania obsiahnuté v matematike a čisto opisné metódy logiky môžu existovať v jednej osobe.

Vedec však chcel povedať, že veda o zákonoch a formách myslenia bola rovnako prísna ako ktorákoľvek z prírodných vied, povedzme matematika a fyzika. Za týmto účelom Boule nezačala označovať čísla ako písmená, ako sa to robí v bežných algebrách, ale výroky, a ukázala, že také rovnice, veľmi podobné algebraickým, môžu vyriešiť otázky o pravdivosti a nepravdivosti výpovedí človeka. Booleovská algebra teda vznikla.

Ale dlho predtým, ako nemecký matematik a filozof Gottfried Leibniz (1646-1716) George George Buhl prvýkrát prišiel s myšlienkou vytvoriť vedu, ktorá by označovala všetky koncepty bežnej hovorovej reči so symbolmi a vytvorila nejakú novú algebru na kombináciu týchto symbolov.

Po vytvorení takejto vedy, podľa Leibniz, sa vedci a filozofi prestanú hádať a kričať na seba, zisťujú pravdu, ale zdvihnú ceruzku a pokojne povedia: „Poďme počítať!“

Dnes sa algebra logiky stala dôležitou súčasťou matematiky. Jednou z jeho úloh je riešenie všetkých druhov rovníc, ktorých číselné pomery sú nahradené abecednými. Každý z vás si pravdepodobne počas svojho života pamätal, ako riešiť rovnice druhého a tretieho stupňa písmenovými koeficientmi. Boole vo svojej novej algebre použil všetky tieto vzorce a pravidlá.

V booleovskej algebre je nové to, že prvky množiny, ktoré sú v nej študované, nie sú čísla, ale výroky. Ak sa pri riešení bežných algebraických rovníc zistí, aké číslo sa rovná neznámemu X, školská algebra hľadá odpoveď na otázku: „Koľko?“

Algebra logiky hľadá odpoveď na otázku: „Je toto alebo toto vyhlásenie označené písmenom X pravdivé?“

Význam a obsah vyhlásenia tu nehrá žiadnu úlohu. Každé tvrdenie môže byť iba pravdivé alebo nepravdivé. Nemôže to byť napoly pravdivá a napoly nepravdivá. Ako príklad si môžeme pripomenúť hodiť veľa mincí.

Do úvahy sa berú iba dva stavy mincí - hlavy alebo chvosty. Po dohode strán je orlom ÁNO a chvosty NIE. V teórii pravdepodobnosti sa nezohľadňujú žiadne ďalšie prechodné body, hoci sú možné. Prevrátená minca môže spadnúť na okraj, prevrátiť sa po podlahe k nohám stoličky alebo stola a zostať vo zvislej polohe alebo dokonca spadnúť do veľkej medzery v podlahe. (Obdobne ako pri elektrických obvodoch sa posledné dve situácie môžu považovať za poruchu vo forme spáleného kontaktu).Ale v týchto dňoch, boolovská algebra, bohužiaľ, nebola široko používaná.

Claude Shannon znovu „objavil“ Buhlovu algebru. V roku 1938, ešte ako študent technologického inštitútu v Massachusetts a Amerike, mladý Claude preukázal, že booleovská algebra je úplne vhodná na analýzu a syntézu reléových a spínacích obvodov.

S pomocou booleovskej algebry je veľmi ľahké vytvoriť elektrický obvod reléového stroja.Ukazuje sa, že potrebujete iba vedieť presne to, čo by mal stroj robiť, to znamená, že na jeho fungovanie musíte mať algoritmus. Preto bol položený základ pre teóriu digitálnych strojov pracujúcich na princípe ÁNO alebo NIE.

Stručne povedané, je to história booleovskej algebry. V nasledujúcich článkoch sa budeme zaoberať jeho základnými zákonmi, príkladmi kontaktných obvodov implementujúcich tieto zákony. Zvážte riešenie tých úloh, ktoré boli zadané na začiatku článku.

Pokračovanie článku: Booleovská algebra. Časť 2. Základné zákony a funkcie

Boris Aladyshkin