"Všetko tečie", alebo Ohmov zákon pre zvedavých

Dokonca aj ten posledný, ktorý už nejaký čas študoval v 10. ročníku, to učiteľovi povie Ohmov zákon - toto je „U sa rovná I-násobku R“. Bohužiaľ, najchytrejší vynikajúci študent povie niečo viac - fyzická stránka Ohmovho zákona mu zostane záhadou pre sedem pečatí. Dovoľujem si podeliť sa so svojimi kolegami o svoje skúsenosti s prezentáciou tejto zdanlivo primitívnej témy.

Predmetom mojej pedagogickej činnosti bol umelecký a humanitárny 10. ročník, ktorého hlavné záujmy, ako čitateľ odhaduje, ležia veľmi ďaleko od fyziky. Preto bola výučba tohto predmetu zverená autorovi týchto línií, ktorí všeobecne hovoria o výučbe biológie. Bolo to pred niekoľkými rokmi.

Lekcia o Ohmovom zákone začína triviálnym tvrdením, že elektrický prúd je pohyb nabitých častíc v elektrickom poli. Ak na nabitú časticu pôsobí iba elektrická sila, potom sa častica zrýchli v súlade s Newtonovým druhým zákonom. A ak je vektor elektrickej sily pôsobiacej na nabitú časticu konštantný na celej trajektórii, je rovnako zrýchlený. Rovnako ako hmotnosť spadá pod vplyv gravitácie.

Ale tu výsadkár padá úplne zle. Ak zanedbáme vietor, potom je jeho rýchlosť konštantná. Dokonca aj študent umeleckej a humanitnej triedy odpovie, že okrem gravitačnej sily pôsobí na padajúci padák ešte jedna sila - sila odporu vzduchu. Táto sila sa v absolútnej hodnote rovná sily príťažlivosti padáka Zemou a je proti nemu v smere. Prečo? Toto je kľúčová otázka lekcie. Po nejakej diskusii sme dospeli k záveru, že ťažná sila sa zvyšuje so zvyšujúcou sa rýchlosťou klesania. Padajúce telo sa preto zrýchľuje na rýchlosť, pri ktorej sa vyrovná gravitácia a odpor vzduchu, a telo ďalej klesá konštantnou rýchlosťou.

Je pravda, že v prípade výsadkárov je situácia o niečo zložitejšia. Padák sa neotvorí okamžite a parašutista sa zrýchli na výrazne vyššiu rýchlosť. A keď sa už padák otvoril, pád začína spomalením, ktoré pokračuje až do vyrovnania gravitačnej sily a sily odporu vzduchu.

Pre padákový náklad s celkovou hmotnosťou m zostupnou konštantnou rýchlosťou proti, môžeme napísať: mg - F (proti) = 0, kde F (proti) Je sila odporu vzduchu považovaná za funkciu rýchlosti pádu. Pokiaľ ide o formu funkcie F (proti) zatiaľ môžeme povedať iba jednu vec: rastie monotónne. Táto okolnosť poskytuje stabilizáciu rýchlosti.

V najjednoduchšom prípade, keď F (proti) = k, konštantná rýchlosť, s ktorou padák padne, sa rovná mg / k. Urobme teraz nejakú konverziu. Nechajte padák padať z výšky h. Potom sa rozdiel v potenciálnych energiách tela pred a po páde rovná mgh = mU, kde U je potenciálna energia tela hmoty vo výške h alebo potenciálny rozdiel gravitačného poľa v počiatočných a konečných bodoch dopadu.

Vzhľadom na vyššie uvedené získame vzorec: F (proti) = mU / h. (1)

A teraz späť k vodiču, ktorým preteká elektrický prúd. Po vodiči sa pohybuje veľké množstvo nabitých častíc, ktoré sa častejšie zrážajú s atómami, tým rýchlejšie lietajú. Analógia so zostupom padáka je celkom priehľadná, jediný rozdiel je v tom, že existuje veľa „padákov“ a nepohybujú sa v gravitačnom, ale v elektrickom poli. Za týchto okolností (1) možno prepísať túto formu: F (proti) = eU / l, (2)

kde e je náboj častíc, U je rozdiel elektrického potenciálu na koncoch vodiča, l je dĺžka vodiča.Prúdová sila sa samozrejme rovná I = neS, kde n je počet nabitých častíc na jednotku objemu, S je plocha prierezu vodiča, je rýchlosť častíc (pre jednoduchosť predpokladáme, že všetky nabité častice sú rovnaké).

Na získanie závislosti I (U) musíte explicitne poznať závislosť F (). Najjednoduchšia možnosť (F = k) okamžite dáva Ohmov zákon (I ~ U):

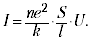
Hodnota sa nazýva vodivosť a jej recipročná hodnota sa nazýva odpor. Na počesť objaviteľa zákona sa odpor zvyčajne vyjadruje v ohmoch.

Hodnota (ne2 / k) sa nazýva špecifická vodivosť a jej inverzná hodnota sa nazýva špecifický odpor. Tieto hodnoty charakterizujú materiál, z ktorého pozostáva vodič. Je dôležité, že vodivosť je úmerná počtu nabitých častíc na jednotku objemu (n). V roztokoch kovov a elektrolytov je tento počet veľký, ale v dielektrike je malý. Počet nabitých častíc na jednotku objemu plynu môže závisieť od aplikovaného poľa (t.j. je to funkcia U), preto sa Ohmov zákon nevzťahuje na plyny.

Pri odvodzovaní Ohmovho zákona sme urobili jeden nezrejmý predpoklad. Uznali sme, že sila, ktorá brzdí pohyb nabitej častice, je úmerná jej rýchlosti. Dalo by sa samozrejme pokúsiť túto myšlienku nejako zdôvodniť, ale experimentálne overenie vyzerá oveľa presvedčivejšie.

Experimentálne overenie tohto predpokladu je samozrejme overením samotného Ohmovho zákona, t.j. proporcionalita U a I. Zdá sa, že to nie je ťažké urobiť: máme voltmeter a ampérmeter! Bohužiaľ, všetko nie je také jednoduché. Našim študentom musíme vysvetliť, že voltmeter, rovnako ako ampérmeter, nemeria napätie, ale prúdovú silu. A máme právo nastaviť volty na stupnici voltmetra iba preto, že spočiatku poznáme Ohmov zákon, ktorý chceme skontrolovať. Potrebujú ďalšie prístupy.

Môžete použiť napríklad nasledujúci nápad. Pripojíme n batérií do série a predpokladáme, že v tomto prípade sa n-krát zvýšilo napätie. Ak je Ohmov zákon pravdivý, potom sa súčasná sila tiež zvýši n krát, kvôli ktorej pomer n / I (n) nebude závisieť od n. Tento predpoklad je odôvodnený skúsenosťami. Je pravda, že batérie majú tiež vnútorný odpor, a preto hodnota n / I (n) rastie pomaly so zvyšujúcim sa n, ale nie je ťažké to napraviť. (G. Ohm sám meral stres iným spôsobom, o ktorom môžu študenti čítať v učebnici G. Ya. Myakisheva a ďalších.)

Pýtame sa: „„ Vo vzdialenej konštelácii Tau Ceti “nie Ohmov zákon, ale zákon veľkého miestneho vedca Akademika X. Podľa zákona X je súčasná sila úmerná druhej mocnine potenciálneho rozdielu na koncoch vodiča. Ako závisí brzdná sila častíc na ich rýchlosti na Tau Ceti? “ Študenti pomocou jednoduchých transformácií dospejú k záveru, že sila je úmerná druhej odmocnine rýchlosti.

A teraz pokračujme v ďalšom procese: pohyb vody v potrubí, na konci ktorého sa vytvárajú rôzne tlaky. Tu máme úplne inú situáciu: nie samostatné pohybujúce sa častice sa trú o stacionárny materiál distribuovaný v celom objeme vodiča, ale vrstvy pohybujúcich sa častíc sa o seba trú. A táto okolnosť zásadne mení všetky fyzické zdôvodnenia.

Dve sily pôsobia na samostatnú vrstvu vody pohybujúcu sa v potrubí:

a) rozdiel tlakových síl na koncoch vrstvy;

b) sila trenia proti susedným vrstvám vody.

Ak sa zistí konštantná rýchlosť vrstvy, potom sú tieto sily rovnaké a nasmerované opačným smerom.

Sila trenia proti susedným vrstvám vody môže spomaliť pohyb iba vtedy, ak sa rôzne vrstvy vody pohybujú rôznymi rýchlosťami. Vo vodiči rýchlosť nabitých častíc nezávisí od toho, či sú na okraji vodiča alebo v jeho strede, ale voda v strede potrubia sa pohybuje rýchlo a pomaly pozdĺž okrajov na samotnom povrchu potrubia, rýchlosť vody je nulová.

Za prúd vody sa môže považovať analóg prúdu, t.j. množstvo vody, ktorá tečie z potrubia za jednotku času. Pretože rýchlosť vody v rôznych vrstvách nie je rovnaká, výpočet prietoku nie je tak jednoduchý.Analógom rozdielu v elektrickom potenciáli je tlakový rozdiel na koncoch potrubia.

Rovnako ako v vodiči s prúdom sa v potrubí s vodou pozoruje priama proporcionalita medzi tlakovým rozdielom na koncoch a prietokom. Koeficient proporcionality je však úplne odlišný. Po prvé, prietok vody závisí nielen od prierezovej plochy potrubia, ale aj od jeho tvaru. Ak je rúrka valcová, potom prietok nie je priamo úmerný ploche prierezu, ale jej štvorcu (t. J. Polomeru štvrtého stupňa). Táto závislosť sa nazýva Poiseuilleov zákon.

Tu je čas pripomenúť si priebeh anatómie, fyziológie a hygieny, študovaný v 9. ročníku. Ľudské telo má veľké množstvo paralelne spojených ciev. Predpokladajme, že jedna z týchto ciev sa rozšírila a jej polomer sa mierne zvýšil, iba dvakrát. Koľkokrát, s rovnakým tlakom na konci cievy, sa zvýši množstvo krvi, ktoré ním prechádza? Plocha prierezu je úmerná druhej mocnine polomeru a druhá mocnina plochy prierezu je úmerná polomeru štvrtého stupňa. Preto, keď sa polomer zdvojnásobí, prietok krvi sa zvýši 16 (!) Krát. Taká je sila zákona Poiseuille, ktorá nám umožňuje vytvoriť veľmi efektívny mechanizmus na prerozdeľovanie krvi medzi orgánmi. Keby elektróny nepretekali krvnými cievami, ich prietok by sa zvýšil iba štyrikrát.

Opis vyššie opísanej témy sa líši od tradičnej témy. Po prvé, tri hodiny sa venujú téme, ktorá sa vzhľadom na súčasný nedostatok hodín môže považovať za neprípustný luxus pre prírodné vedy. Je to však odôvodnené skutočnosťou, že je možné celkom jednoducho a populárne odhaliť fyzikálny význam zákona a vybaviť študentov metodikou, ktorú môžu použiť na analýzu rôznych fyzikálnych procesov: pád tela vo vzduchu, pohyb tekutiny v potrubí, pohyb nabitých častíc pozdĺž vodiča a neskôr pri analýze priechodu elektrického prúdu vákuom a plynmi.

Tento prístup sa nazýva intradisciplinárna integrácia. S jej pomocou sme demonštrovali študentom spoločné črty vo vzdialených, na prvý pohľad, častiach fyziky, ukázali sme, že fyzika nie je „zväzkom“ „fyzikálnych zákonov“, ktoré spolu nesúvisia, ale sú štíhlou budovou. To isté samozrejme platí aj pre iné vedecké disciplíny. Zdá sa teda, že iracionálne plytvanie školiacimi hodinami sa úplne vypláca.

Prečítajte si tiež:Ako používať multimeter