kategória: Najlepšie články » Praktická elektronika
Počet zobrazení: 32001
Komentáre k článku: 2
Kondenzátory v elektronických obvodoch
V predchádzajúcich článkoch sme stručne hovorili o činnosti kondenzátorov v striedavých obvodoch, o tom, ako a prečo kondenzátory prechádzajú striedavým prúdom (pozri - Kondenzátory striedavého prúdu). V tomto prípade sa kondenzátory nezohrievajú, nie je im pridelená energia: v jednej polovici vlny sínusoidu sa kondenzátor nabíja a v druhom sa prirodzene vybíja, pričom prenáša uloženú energiu späť do zdroja prúdu.
Tento spôsob prenosu prúdu vám umožňuje nazývať kondenzátor voľným odporom, a preto kondenzátor pripojený k zásuvke nespôsobuje otáčanie počítadla. A to všetko preto, že prúd v kondenzátore je v predstihu pred presne 1/4 času, keď naň bolo použité napätie.
Ale tento fázový pokrok umožňuje nielen „trik“ počítadla, ale tiež umožňuje vytvoriť rôzne obvody, napríklad generátory sínusových a pravouhlých signálov, časové oneskorenia a rôzne frekvenčné filtre.
V priebehu tohto príbehu bude potrebné niekedy pripomenúť, čo už bolo povedané, zhrnúť. Pomôže to nevrátiť sa k predchádzajúcim článkom, aby sme si pripomenuli jednoduchý vzorec alebo jednoducho „čo je to?“
Paralelné a sériové zapojenie kondenzátorov
Pri paralelnom pripojení kondenzátorov je celková kapacita jednoducho aritmetickým súčtom kapacít. Pri tomto zahrnutí bude samozrejme celková kapacita väčšia ako kapacita najväčšieho kondenzátora. Ctotal = C1 + C2 + C3 + ... + Cn.
V prípade sériového pripojenia je celková kapacita menšia ako kapacita najmenšej.
1 / Celkom = 1 / C1 + 1 / C2 + 1 / C3 + ... + 1 / Cn.
Ak sú dva rovnaké kondenzátory zapojené do série, celková kapacita sa bude rovnať polovici kapacity jedného: napríklad, keď sa spoja dva kondenzátory po 1 uF, celková kapacita bude 0,5 uF.
Kapacita Xc
Tu je všetko, rovnako ako pri pripájaní odporov, presným opakom: sériové pripojenie znižuje celkovú kapacitu, zatiaľ čo paralelné zosilnenie zvyšuje. Na túto okolnosť by sa nemalo zabúdať pri pripájaní kondenzátorov, pretože zvýšenie kapacity vedie k zníženiu kapacity Xc.
Xc = 1/2 * π * f * C.
Z hľadiska matematiky je to celkom prirodzené, pretože kapacita C je vo menovateli zlomku. Mimochodom, frekvencia f je na rovnakom mieste, takže zvýšenie frekvencie tiež vedie k zníženiu kapacity Xc. Fyzický význam tohto je ten, že prostredníctvom toho istého kondenzátora je lepšie, bez zábran, že prechádzajú vysoké frekvencie. O tom sa bude diskutovať o niečo neskôr, pokiaľ ide o filtre dolného a horného priechodu.
Ak vezmeme kondenzátor s kapacitou 1 μF, potom pre frekvenciu 60 Hz bude jeho Xc 2653 Ohmov a pre frekvenciu 400 Hz má rovnaký kondenzátor Xc iba 398 Ohmov. Tí, ktorí chcú, môžu tieto výsledky skontrolovať pomocou vzorca, ktorý nahradí π = 3,14, frekvenciu v hertzoch a kapacitu v faradách. Výsledok bude potom v ohmoch. Všetko musí zodpovedať systému SI!
Kondenzátory sa však používajú nielen ako tlmiace odpory s voľným tlmením alebo v usmerňovacích filtroch. Bez ich účasti obvody pre nízko a vysokofrekvenčné generátory, rôzne prevodníky tvaru vlny, rozlišovacie a integračné obvody, zosilňovače a ďalšie schémy.
Ďalej sa budú brať do úvahy rôzne elektrické signály, s ktorými kondenzátory musia pracovať. Po prvé, jedná sa o periodické signály vhodné na pozorovanie pomocou osciloskop.
Obdobie a frekvencia kmitov
Periodická oscilácia sa preto nazýva periodická, ktorá bez prestania opakuje rovnakú formu, napríklad jednu sínusovú osciláciu. Trvanie tohto úplného kolísania sa presne nazýva perióda T a meria sa v sekundách, milisekundách, mikrosekundách.Moderná elektronika sa dokonca zaoberá nanosekundami (miliardtina sekundy).
Počet periód za sekundu sa nazýva frekvencia (ako často) kmitov f a vyjadruje sa v hertzoch. 1Hz je frekvencia, pri ktorej sa vykoná jedna oscilácia, jedna celá perióda za 1 sekundu. Pomer periódy a frekvencie je vyjadrený jednoduchým vzorcom T = 1 / f.
V súlade s vedomím periódy kmitania je preto veľmi jednoduché vypočítať frekvenciu f = 1 / T.
Takto sa vypočíta frekvencia pri meraní osciloskopom: vypočíta sa počet buniek v perióde vynásobený dobou trvania jednej bunky a perióda sa získa napríklad v mikrosekundách. A aby zistili frekvenciu, jednoducho použili posledný vzorec.
obyčajný elektronický osciloskop Umožňuje pozorovať iba periodické signály, ktoré je možné synchronizovať s frekvenciou rozmítania, aby ste získali statický obrázok vhodný na výskum. Ak odošlete signál do hudobného programu na vstup osciloskopu, nebudete môcť zastaviť žiadny obrázok. Na pozorovanie takýchto signálov sa používajú pamäťové osciloskopy.
Keď sa perióda meria v milisekundách, frekvencia sa získa v kilohertzoch, za periódu meranú v mikrosekundách sa frekvencia už vyjadrí v megahertzoch. To je, ak nedodržíte požiadavky systému SI: perióda v sekundách, frekvencia v hertzoch.
Nesinusové vibrácie
Ako už bolo spomenuté, sínusová vlna je najbežnejšia a je vhodná na štúdium a praktické využitie periodickej krivky. V priemyselných podmienkach sa získava pomocou elektrických generátorov, napríklad vo vodných elektrárňach. V elektronických zariadeniach sa používajú vibrácie najrôznejších tvarov.
V zásade ide o tri formy: sínusové, obdĺžnikové a trojuholníkové, ako je to znázornené na obrázku 1. Prúd aj napätie môžu mať taký tvar, preto obrázok zobrazuje iba časovú os, ordinovaná os je ponechaná bez mena.
Takéto kmity sú generované špeciálnymi elektronickými obvodmi. Obdĺžnikové a trojuholníkové signály sa často nazývajú impulzné. Existuje však veľa elektronických obvodov, ktoré vykonávajú konverziu signálu: napríklad zo sínusoidu môže byť vyrobený napríklad obdĺžnik.
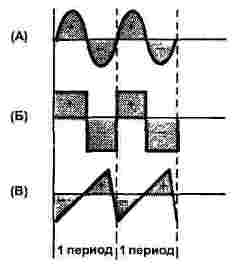
Obrázok 1
Pre všetky tri signály, obrázok ukazuje dve periódy, všetky signály majú rovnakú frekvenciu.
Spektrum nesínusových signálov
Akýkoľvek elektrický signál môže byť reprezentovaný ako meranie amplitúdy v určitom časovom okamihu. Frekvencia týchto vzoriek sa nazýva vzorkovacia frekvencia a najmenej dvakrát vyššia ako horná frekvencia meraného signálu. Potom z týchto vzoriek môžete obnoviť pôvodný signál. Táto metóda sa používa napríklad pri digitálnom zázname zvuku. Táto metóda sa nazýva aj časová analýza.
Ďalšia metóda predpokladá, že akýkoľvek signál, dokonca aj obdĺžnikový, môže byť predstavovaný ako algebraický súčet sínusoidov s rôznymi frekvenciami a fázami. Táto metóda sa nazýva frekvenčná analýza. To, čo bolo povedané „s rôznymi frekvenciami“, však nie je úplne pravda: volebné sínusoidy sa nazývajú harmonické a ich frekvencie sa riadia určitými zákonmi.
Sinusová vlna, ktorej frekvencia sa rovná frekvencii štvorcovej vlny, sa nazýva základná alebo prvá harmonická. Rovnomerné harmonické kmity sa získajú vynásobením základnej frekvencie párnym číslom a nepárne harmonické, nepárne.
Ak teda prvá harmonická má frekvenciu 1 000 Hz, potom druhá je 2 000 Hz, štvrtá je 4 000 Hz atď. Odd harmonické budú mať frekvencie 3000 Hz, 5 000 Hz. Okrem toho je každá harmonická amplitúda menšia ako hlavná: čím vyššia je harmonická, tým menšia je amplitúda.
V hudbe sa harmonické nazývajú tóny. Sú to tí, ktorí tvoria farbu zvuku, umožňujú rozlíšiť husle od klavíra a gitary od saxofónu. Nedovoľujú zamieňať mužský a ženský hlas ani odlíšiť Petrov od Ivanov. A len sínusoid samotný už nemôže byť rozložený alebo zostavený z akýchkoľvek signálov.
Obrázok 2 zobrazuje konštrukciu pravouhlého impulzu.
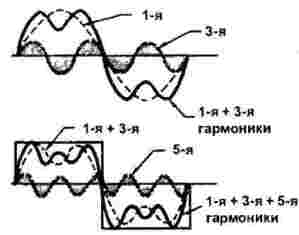
Obrázok 2
Prvá a tretia harmonická sú zobrazené v hornej časti obrázku. Je ľahké vidieť, že v jednej perióde prvého harmonického tri periódy tretieho prechodu. V tomto prípade je amplitúda tretej harmonickej jedna tretina prvej. Suma prvých a tretích harmonických je tu tiež znázornená.
Ďalej, spolu so súčtom 1 a 3 harmonických, sa zobrazuje ďalších 5 harmonických: za periódu obdĺžnikového signálu dokáže presne päť periód. V tomto prípade je jeho amplitúda ešte menšia, presnejšie presne 1/5 hlavnej (prvej) amplitúdy. Človek by si však nemal myslieť, že všetko končí piatou harmonickou: na obrázku sa jednoducho nedá ukázať, v skutočnosti je toho omnoho viac.
Tvorba pílových a trojuholníkových signálov, znázornená na obrázku 3, je o niečo zložitejšia, ak sa v predchádzajúcom prípade zúčastnili iba nepárne harmonické, vstupujú do hry dokonca aj harmonické.
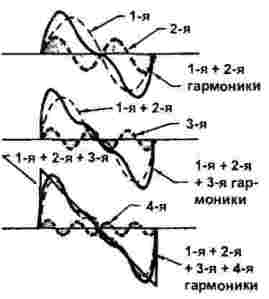
Obrázok 3
Môžeme teda konštatovať, že pomocou mnohých harmonických je syntetizovaný signál akéhokoľvek tvaru a počet a typ harmonických závisí od tvaru vlny, ako je znázornené na obrázkoch 2 a 3.
Pri oprave a nastavení elektronických zariadení sa osciloskop používa na štúdium elektrických signálov. To vám umožní zvážiť formu periodických signálov, ich amplitúdu, zmerať dobu opakovania. Harmonické hodnoty znázornené na obrázkoch 2 a 3 však nie sú viditeľné.
Aj keď napríklad pripojíte elektrickú gitaru k osciloskopu, potiahnete jeden reťazec, na obrazovke sa objaví sínusoid, je to tiež prvý harmonický. V tomto prípade nie je možné hovoriť o žiadnych podtextoch. Rovnaký sínusoid bude mať za následok, že vyhodíte do rúry alebo do drážky pred mikrofónom.
Ako získať obdĺžnikové impulzy
Keď sa zoznámime s elektrickými signálmi, musíme si vybaviť kondenzátory, s ktorými článok začal. Najprv by ste sa mali zoznámiť s jedným z klasických elektronických obvodov - multivibrátor, (Obrázok 4) generuje pravouhlé impulzy. Okruh je tak klasický, že okamžite začne pracovať bez potreby akýchkoľvek nastavení alebo úprav.
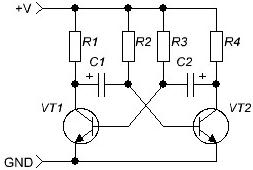
Obrázok 4
Multivibrátor je dvojstupňový zosilňovač pokrytý pozitívnou spätnou väzbou. Ak sú kolektory zaťaženia kolektora R1 = R4, základné odpory R2 = R3 a kondenzátory C1 = C2 rovnaké, multivibrátor sa nazýva symetrický a generuje impulzy štvorcovej vlny typu meandrov - doba trvania impulzu sa rovná dobe trvania pauzy.
Pracovný cyklus takýchto impulzov (pomer periódy k trvaniu impulzov) sa rovná dvom. V schémach v anglickom jazyku je všetko presne opačné: nazývajú to pracovný cyklus. Vypočíta sa ako pomer trvania impulzu k obdobiu jeho sledu a vyjadruje sa v percentách. Pre meander je teda pracovný cyklus 50%.
Je počítač správny?
Názov multivibrátor navrhol holandský fyzik van der Pol, pretože spektrum pravouhlého signálu obsahuje veľa harmonických. Môžete to overiť, ak môžete umiestniť rádiový prijímač, ktorý pracuje v oblasti stredných vĺn, do blízkosti multivibrátora, ktorý pracuje aj na zvukovej frekvencii: vytie vychádzajú z reproduktora. To naznačuje, že okrem zvukovej frekvencie multivibrátor emituje aj vysokofrekvenčné oscilácie.
Na určenie generačnej frekvencie je možné použiť vzorec f = 700 / (C1 * R2).
Pri tejto forme vzorca je kapacita kondenzátora v mikrofaradách (μF), odpor v kiloohmoch (KΩ), výsledok v hertzoch (Hz). Frekvencia je teda určená časovou konštantou obvodu C1 * R2, zaťaženie kolektora neovplyvňuje frekvenciu. Ak vezmeme C1 = 0,02 μF, R2 = 39 KΩ, dostaneme f = 700 / (0,02 * 39) = 897,4 Hz.
Multivibrátor vo veku počítačov a počítačov mikroprocesory Podľa tejto schémy sa takmer nikdy nepoužíva, hoci môže byť vhodná na rôzne experimenty. Najskôr pomocou počítačov. Takto vyzerá multivibrátorový obvod zostavený v programe Multisim. Tu je tiež znázornené spojenie osciloskopu.
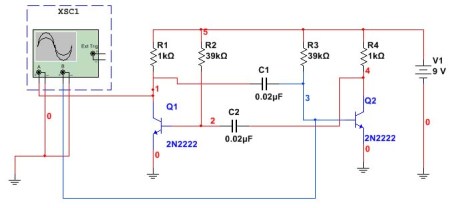
Obrázok 5
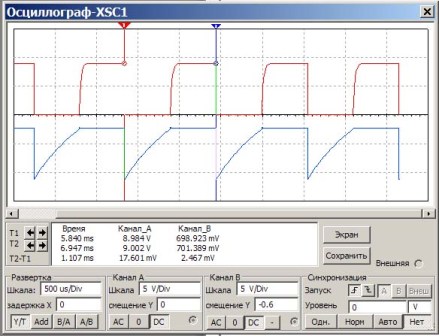
V tomto obvode sú kondenzátory a odpory nainštalované ako v predchádzajúcom príklade. Úlohou je skontrolovať výpočet podľa vzorca, či sa dosiahne rovnaká frekvencia. Za týmto účelom zmerajte periódu impulzov a potom ich prepočítajte podľa frekvencie. Výsledok multisim osciloskopu je znázornený na obrázku 6.
Obrázok 6
Niektoré vysvetlenia k obrázku 6.
Na obrazovke osciloskopu červený impulz zobrazuje impulzy na kolektore tranzistorov a modrý na základniach. Pod obrazovkou vo veľkom bielom okne čísla ukazujú výsledky merania. Zaujíma nás stĺpec „Čas“. Čas sa meria pomocou ukazovateľov T1 a T2 (červené a modré trojuholníky nad obrazovkou).
Teda perióda opakovania impulzov T2-T1 = 1,107 ms je zobrazená celkom presne. Zostáva iba na výpočet frekvencie f = 1 / T = 1/1 107 * 1 000 = 903 Hz.
Výsledok je takmer rovnaký ako vo výpočte podľa vzorca, ktorý je uvedený o niečo vyšší.
Kondenzátory je možné používať nielen samostatne: v kombinácii s odpormi vám umožňujú jednoducho vytvárať rôzne filtre alebo vytvárať obvody s fázovým posunom. O tom sa však budeme zaoberať v nasledujúcom článku.
Pokračovanie článku: Kondenzátory v elektronických obvodoch. Časť 2
Boris Aladyshkin
Pozri tiež na electro-sk.tomathouse.com
: